Introducción
Diseño Experimental
Edimer David Jaramillo
2024-08-09
Método científico
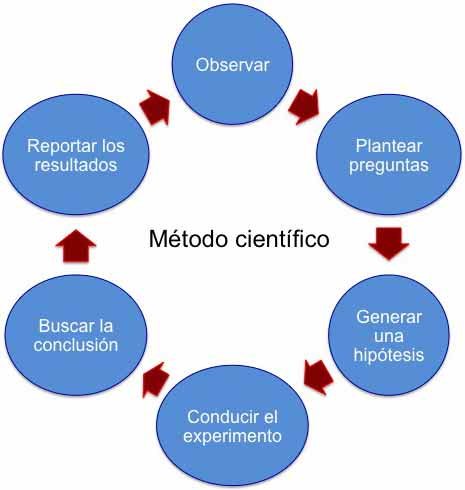
Método PPDAC
Inferencia estadística
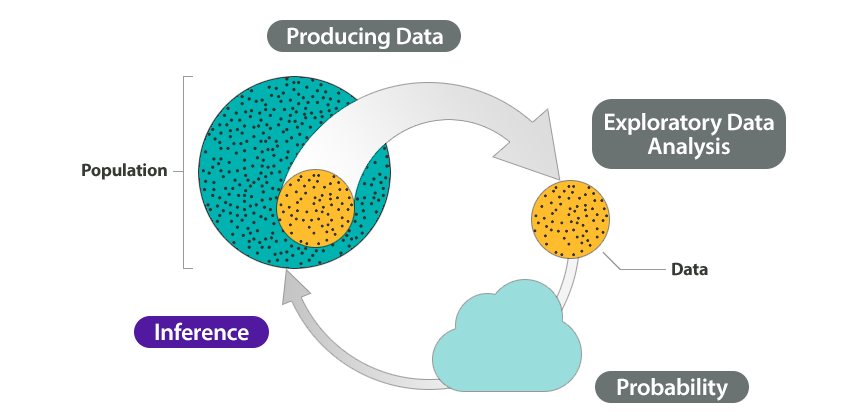
Proceso de análisis de datos
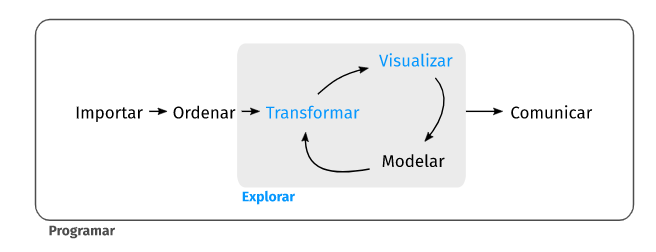
Planificación e implementación de un estudio
- Objetivo del estudio: ¿Qué esperan aprender o entender las partes interesadas en el experimento?
- Selección de respuestas: ¿Qué variable (s) se utilizarán para evaluar el objetivo del estudio?
- Selección de tratamientos y otras covariables:
- Factor: variable que se cree afectará a la variable respuesta
- Tipos de factores: cuantitativos y cualitativos
- Factores cuantitativos: toman valores en un rango continuo
- Factores cualitativos: los valores de una factor se denominan niveles, un tratamiento es un nivel del factor o una combinación de niveles de varios factores
- Desarrollar un plan de estudio: ¿Cómo se recopilarán los datos? ¿Cada cuánto se realizarán mediciones? ¿Quién es la unidad experimental?
- Recopilación de datos: describa con detalle los valores reales de los factores y cómo se registrará la variable respuesta
- Análisis de datos: realice análisis de datos para evaluar la relación entre los factores y las variables respuesta.
- Extraer conclusiones: el análisis de datos deberá ser de utilidad para extraer conclusiones, armar conjeturas o nuevas hipótesis y establecer recomendaciones.
Algunas preguntas de interés…
- ¿Cuál es la proporción de semillas germinadas para la marca X?
- ¿Existen diferencias en la proporción de frutas afectadas para dos casas comerciales que proveen un producto que inhibe el efecto de plagas?
- ¿Cuál es el promedio del rendimiento (en toneladas por hectárea) para el cultivo de café en Colombia?
- ¿Existen diferencias en el promedio de producción de leche al suministrar el aditivo A vs aditivo B en la dieta de las vacas?
- ¿Existe alguna relación entre la cantidad de forraje verde consumido vs la producción de leche?
- ¿Existe alguna relación entre la edad de parto y el peso de los animales?
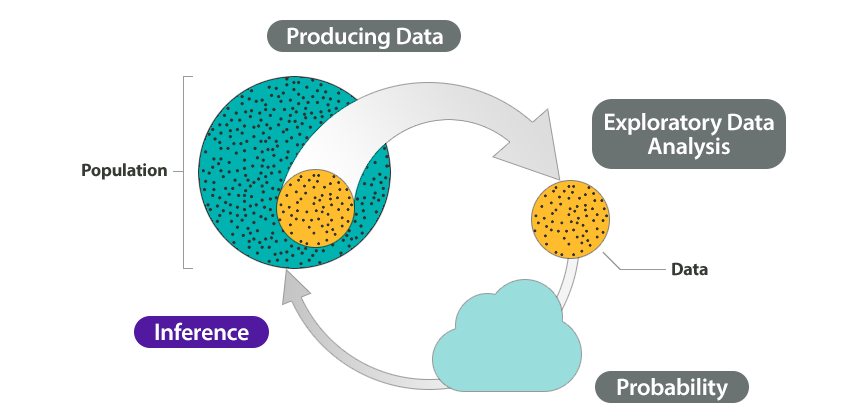

Parámetros de interés en la regresión
\[\hat{y} = \hat{\beta_0} + \hat{\beta_1}X_{i1} + \hat{\beta_2}X_{i2} + ... + \hat{\beta_{p-1}}X_{i_{(p-1)}} + \hat{\epsilon}\]
\[\beta = (X^TX)^{-1}X^Ty\]
| Parámetro Poblacional | Notación | Estadístico | Estimación | Hipótesis |
|---|---|---|---|---|
| Pendiente de regresión poblacional | \(\beta_i\) | \(\hat{\beta_i}\) | Pendiente de regresión muestral | \[H_0: \beta_i = 0 \\ H_1: \beta_i \neq 0\] |
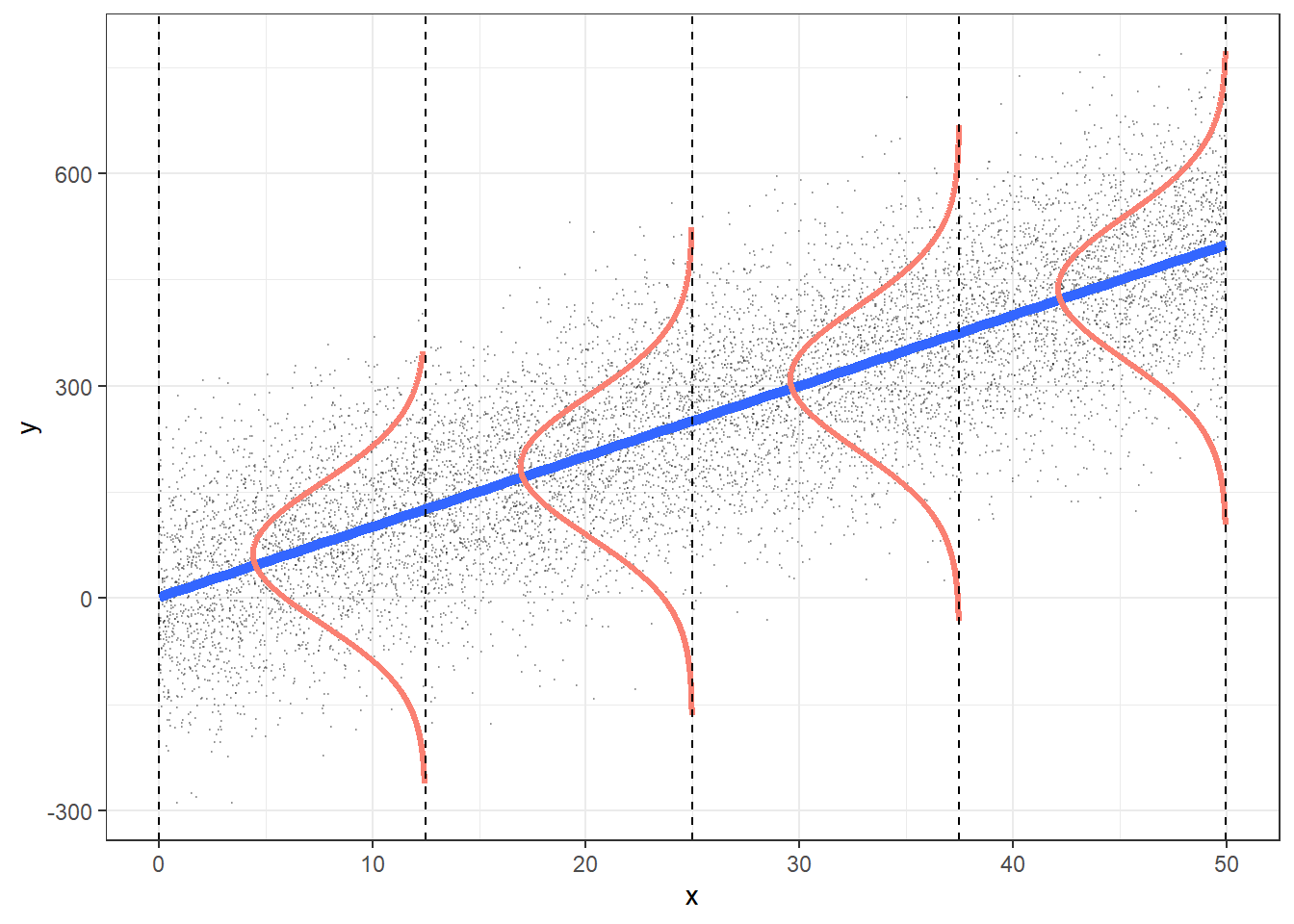
Supuestos matemáticos de modelos lineales
- Normalidad
- Homocedasticidad
- Independencia
- Linealidad
Otros parámetros de interés
| Parámetro Poblacional | Notación | Estadístico | Estimación | Hipótesis |
|---|---|---|---|---|
| Proporción poblacional | \(p\) | \(\hat{p}\) | Proporción muestral | \[H_0: p = \theta \\ H_1: p \neq \theta\] |
| Media poblacional | \(\mu\) | \(\bar{x}\) | Media muestral | \[H_0: \mu = \theta \\ H_1: \mu \neq \theta\] |
| Diferencia de proporciones poblacionales | \(p_1 - p_2\) | \(\hat{p_1} - \hat{p_2}\) | Diferencia de proporciones muestrales | \[H_0: p_1 - p_2 = 0 \\ H_1: p_1 - p_2 \neq 0\] |
| Diferencia de medias poblacionales | \(\mu_1 - \mu_2\) | \(\bar{x_1} - \bar{x_2}\) | Diferencia de medias muestrales | \[H_0: \mu_1 - \mu_2 = 0 \\ H_1: \mu_1 - \mu_2 \neq 0\] |
Tipos de modelos

Métodos estadísticos

El arte de la experimentación
¿Por qué hacer un experimento?
- Determinar las principales causas de variación en una respuesta medida
- Encontrar las condiciones que dan lugar a una respuesta máxima o mínima
- Obtener un modelo matemático para predecir respuestas futuras
Técnicas fundamentales
- Replicación
->Incrementa precisión - Bloqueo
->Incrementa precisión - Aleatorización
->Reduce el sesgo

- Réplica
- Repetición
- Unidad experimental
- Factor (fuente de variación)
- Tratamiento
- Bloque
- Efectos aditivos
- Efectos multiplicativos (interacción)
¡Gracias!

