Regresión Lineal Múltiple

Diseño Experimental

Edimer David Jaramillo

2024-10-03

Regresión Lineal Múltiple

---

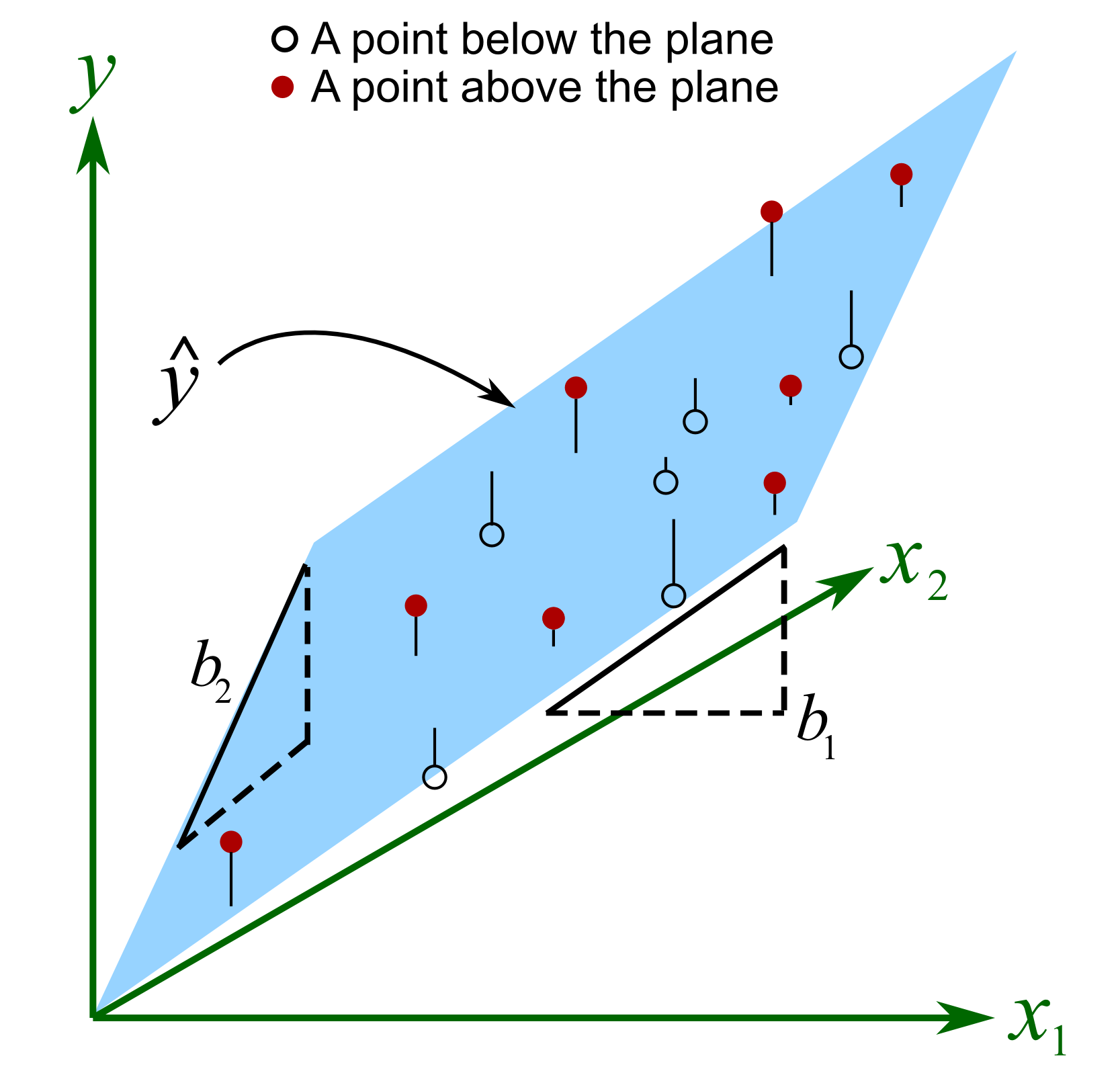
Modelos

---

Modelo Lineal

\[y = b + mx \\\]

Modelo Lineal (Estadística)

\[y = \beta_0 + \beta_1X_i + \epsilon \\ \hat{y} = \hat{\beta_0} + \hat{\beta_1}X_i + \hat{\epsilon}\]

Modelo Lineal Múltiple

\[\hat{y} = \hat{\beta_0} + \hat{\beta_1}X_{i1} + \hat{\beta_2}X_{i2} + ... + \hat{\beta_{p-1}}X_{i_{(p-1)}} + \hat{\epsilon}\]

Aproximación matricial

---

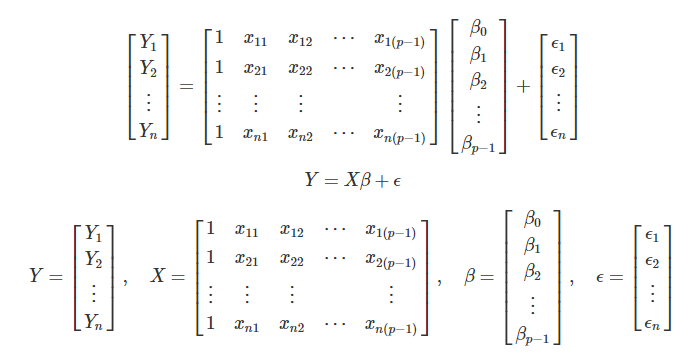
• Estimación por mínimos cuadrados:

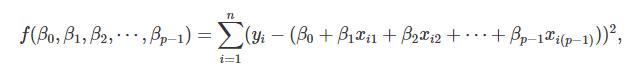
\[\beta = (X^TX)^{-1}X^Ty\]

Hiperplano

---

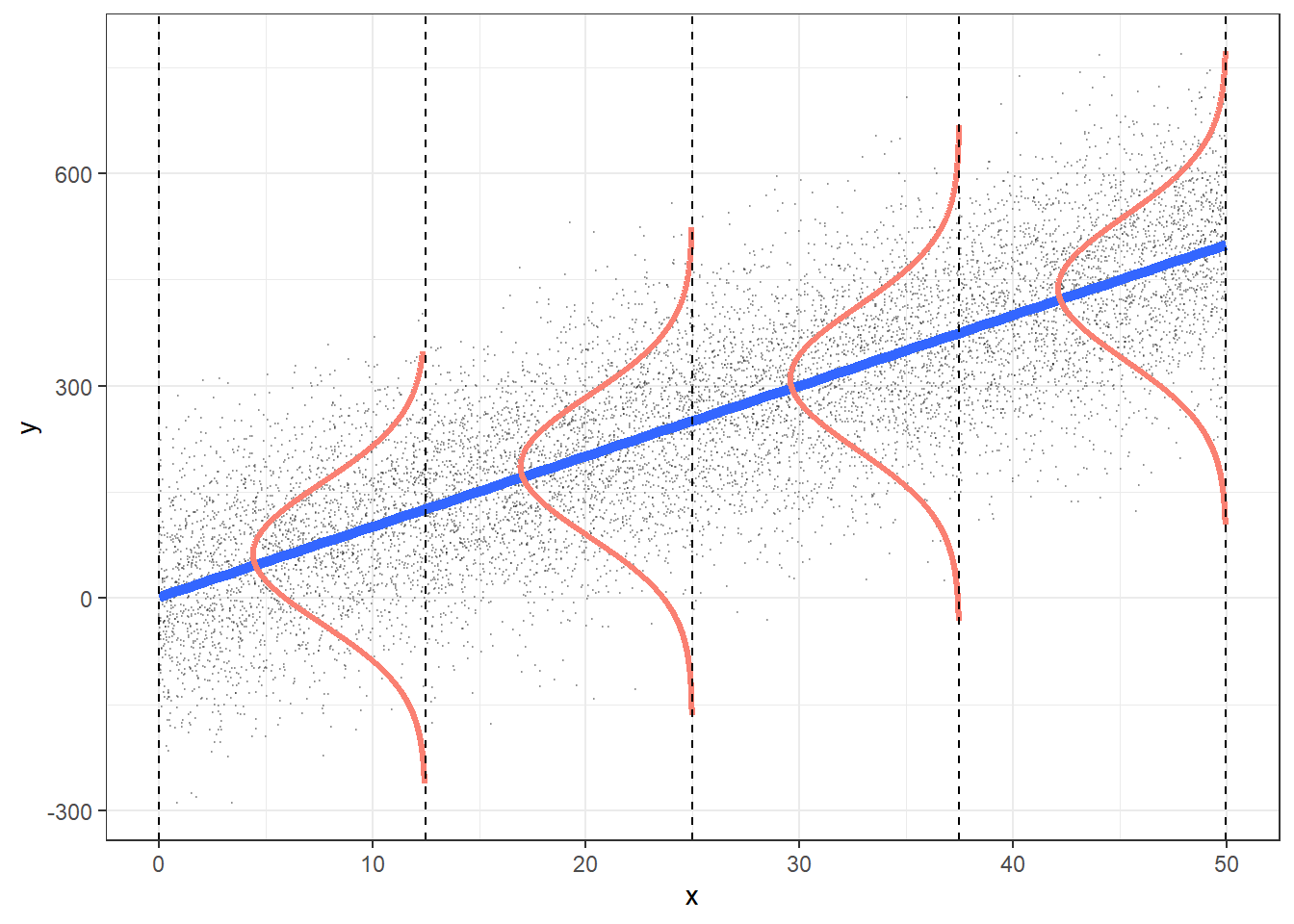
Supuestos matemáticos

---

• Normalidad
• Homocedasticidad
• Indepedencia
• Linealidad

Predictores numéricos

---

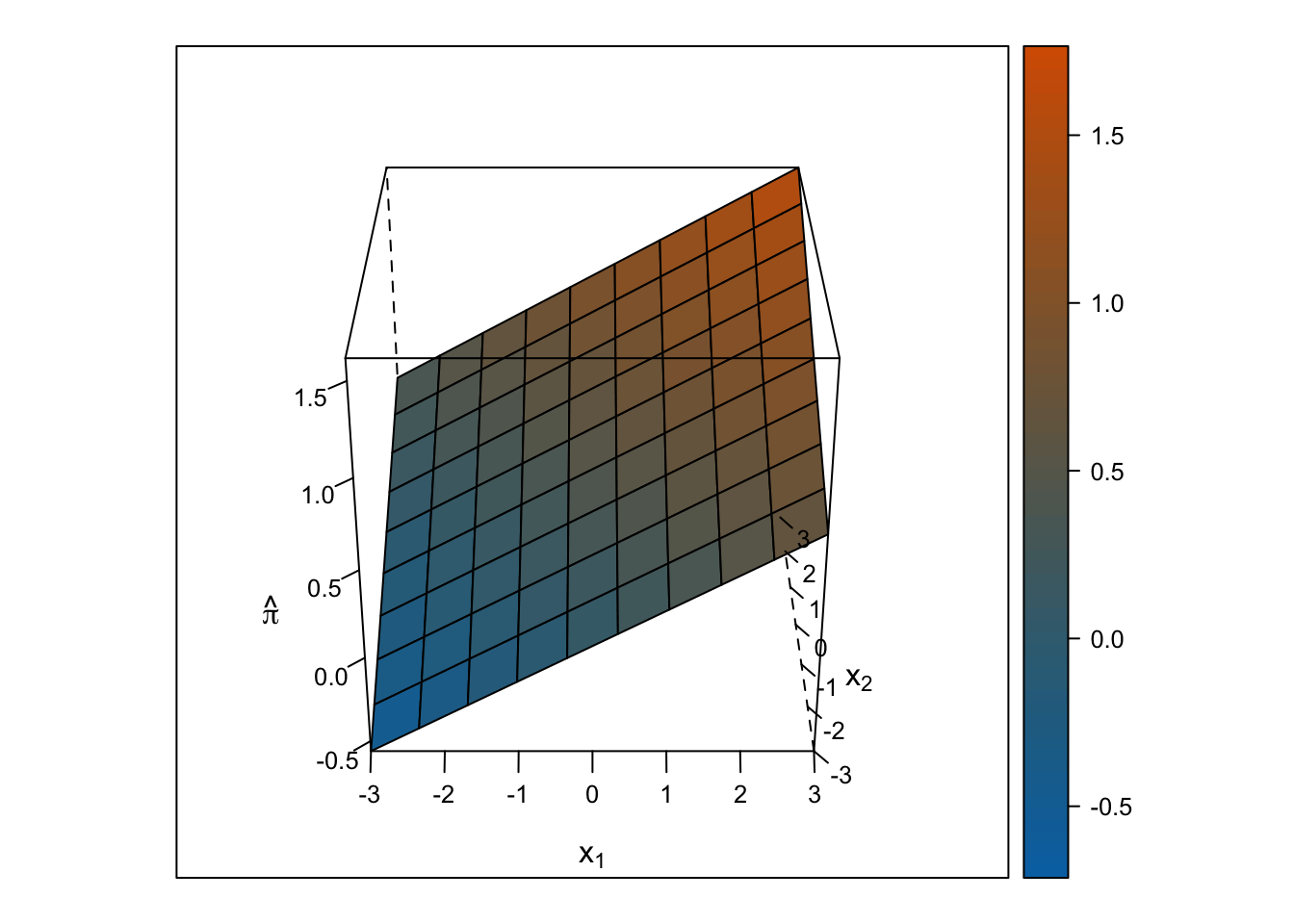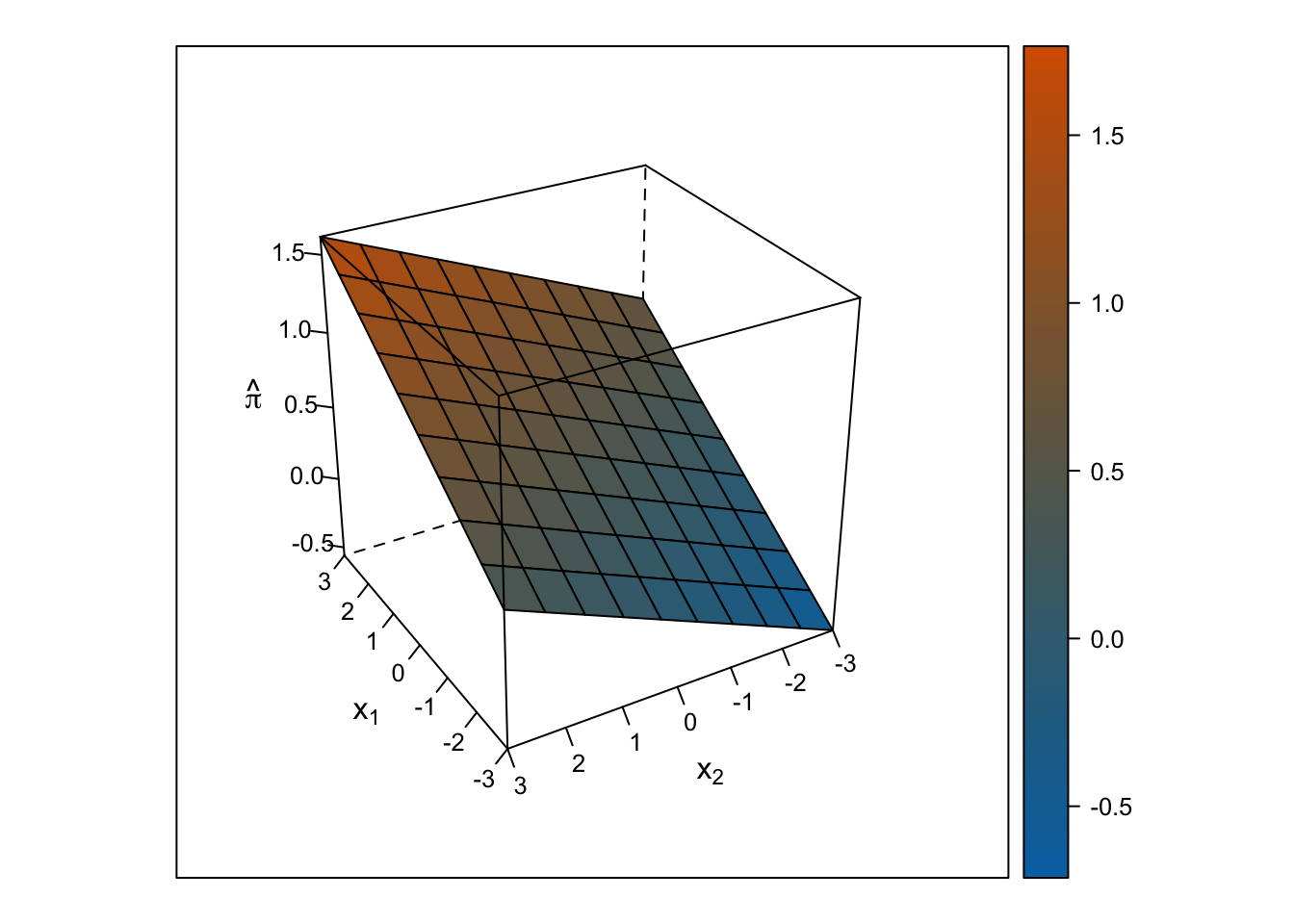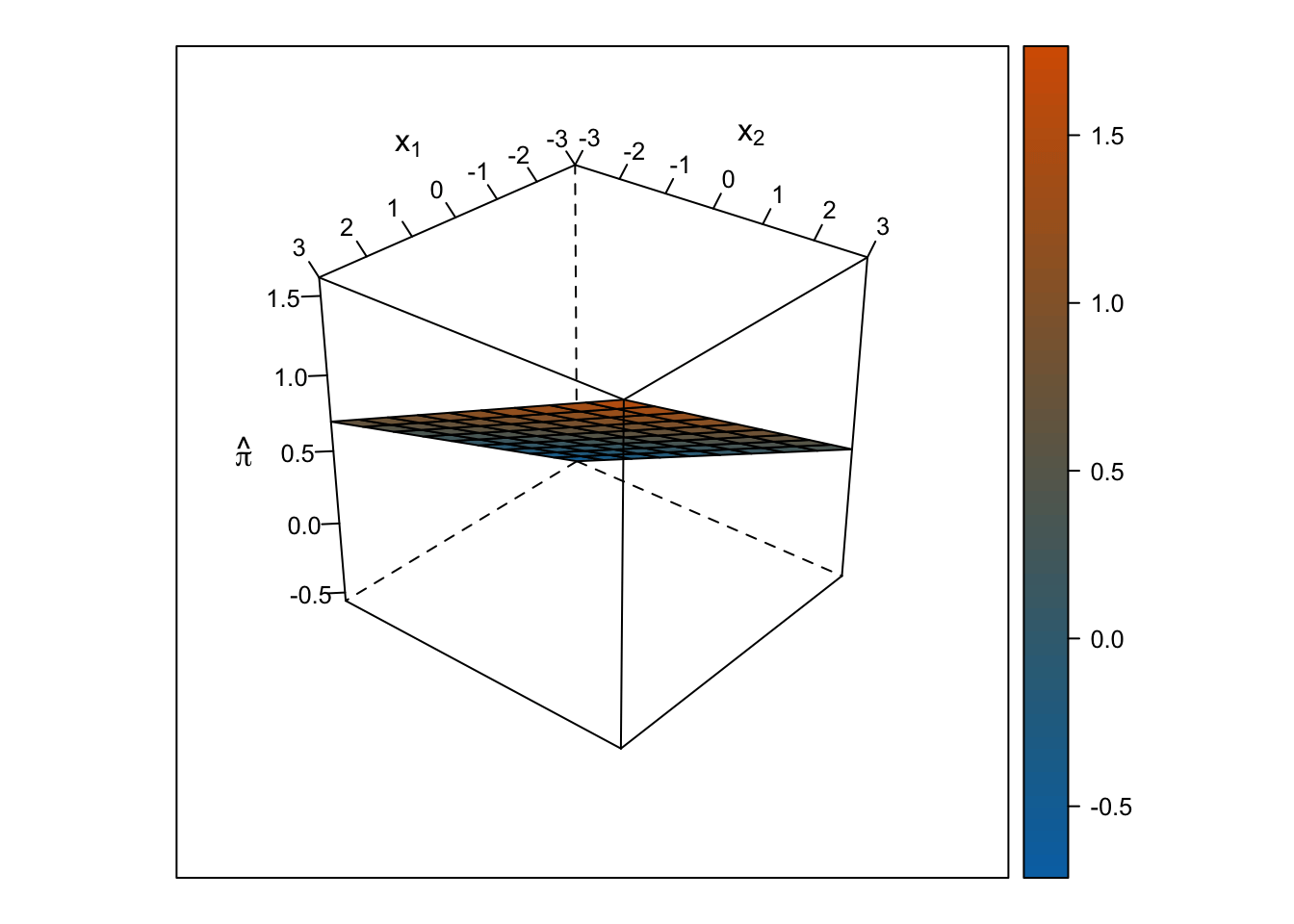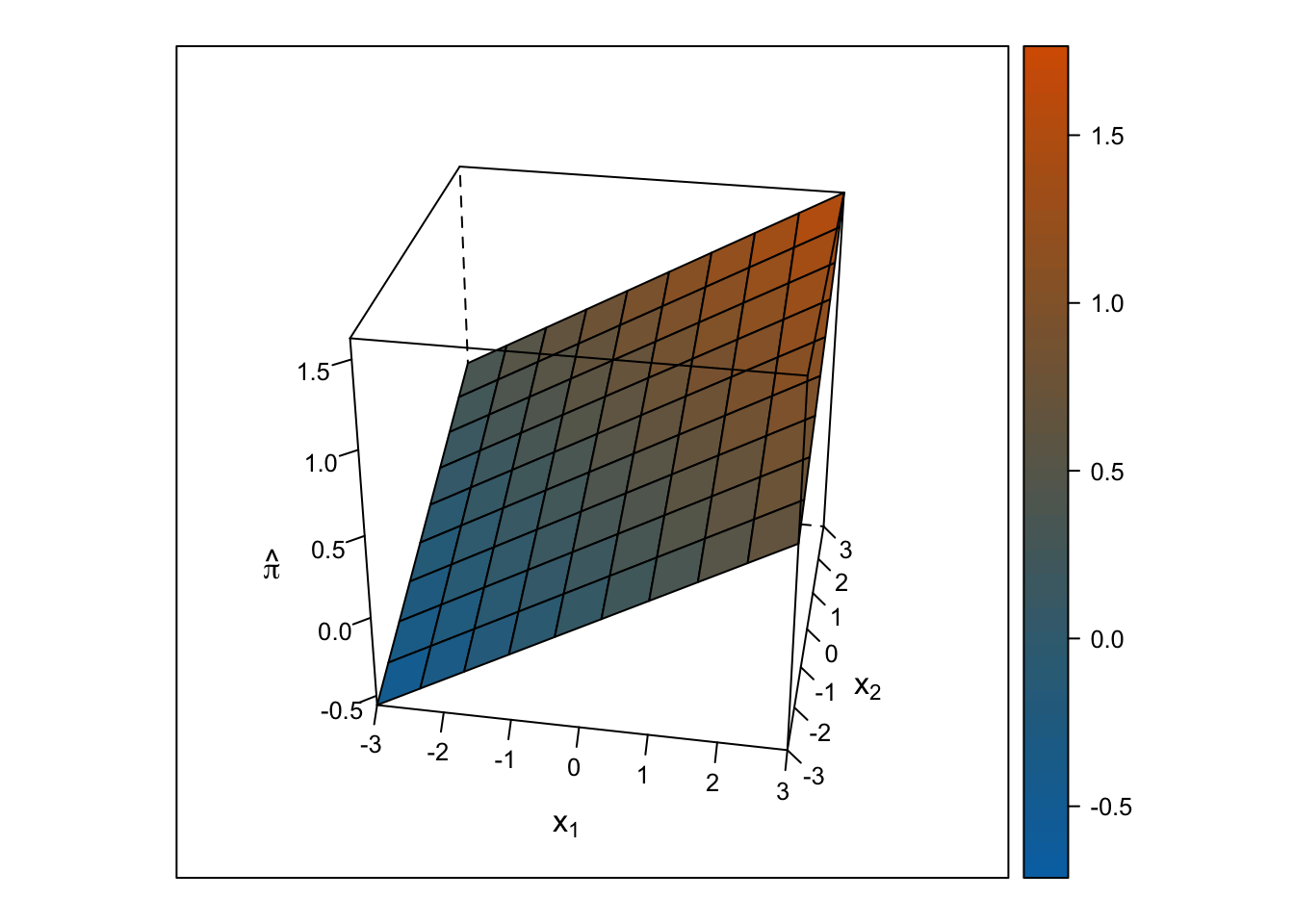
Predictores categóricos

---

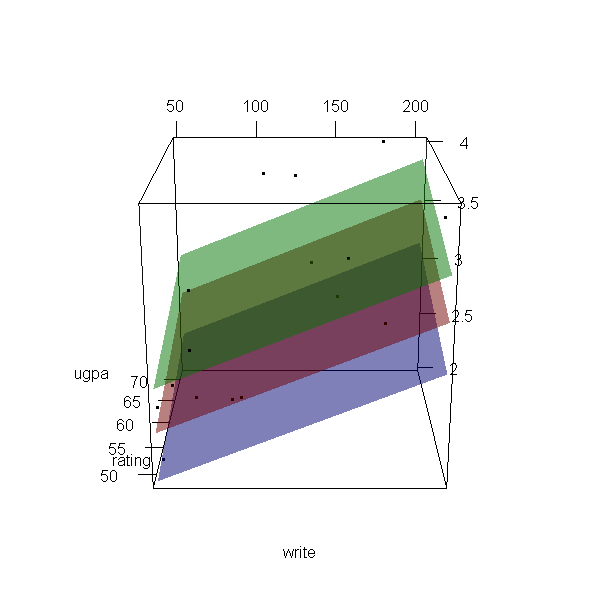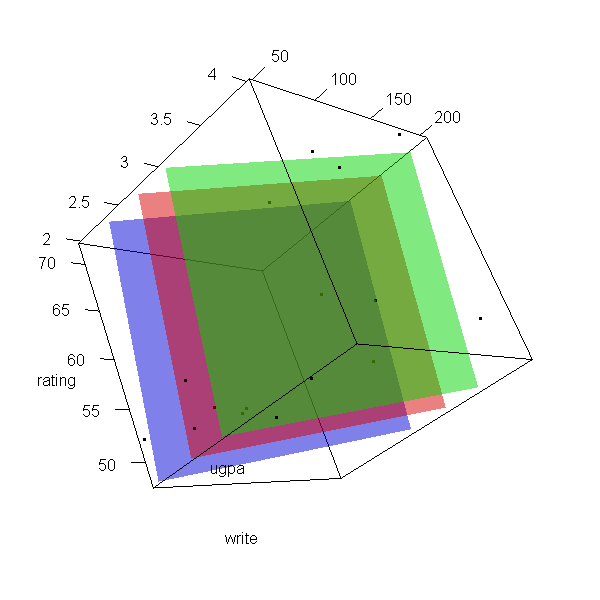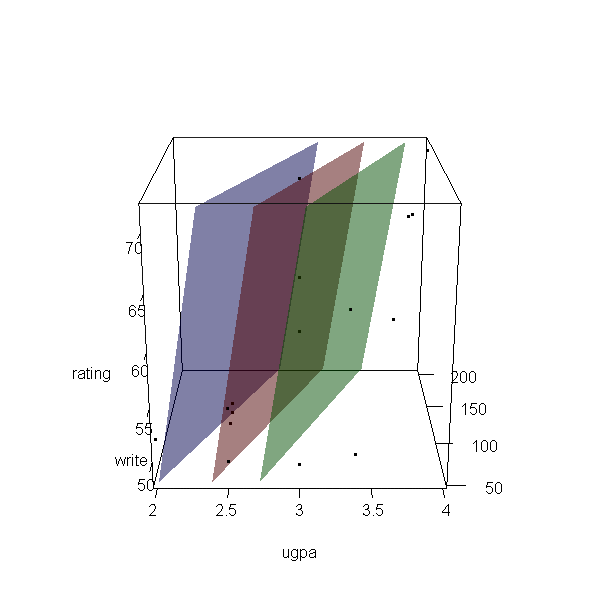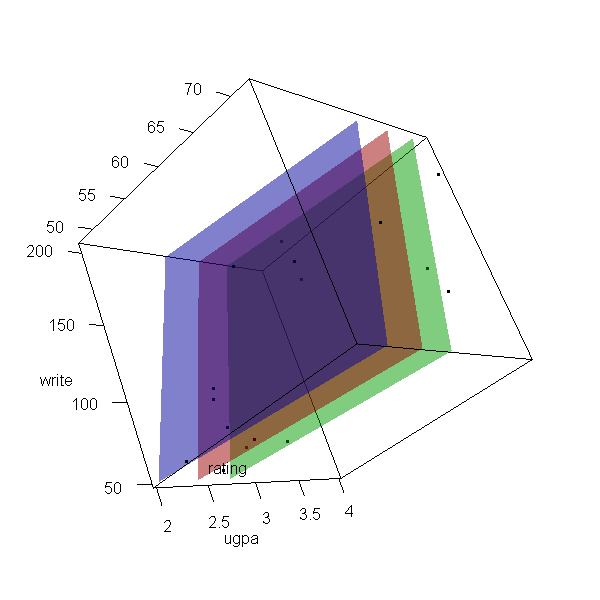
Interacciones

---

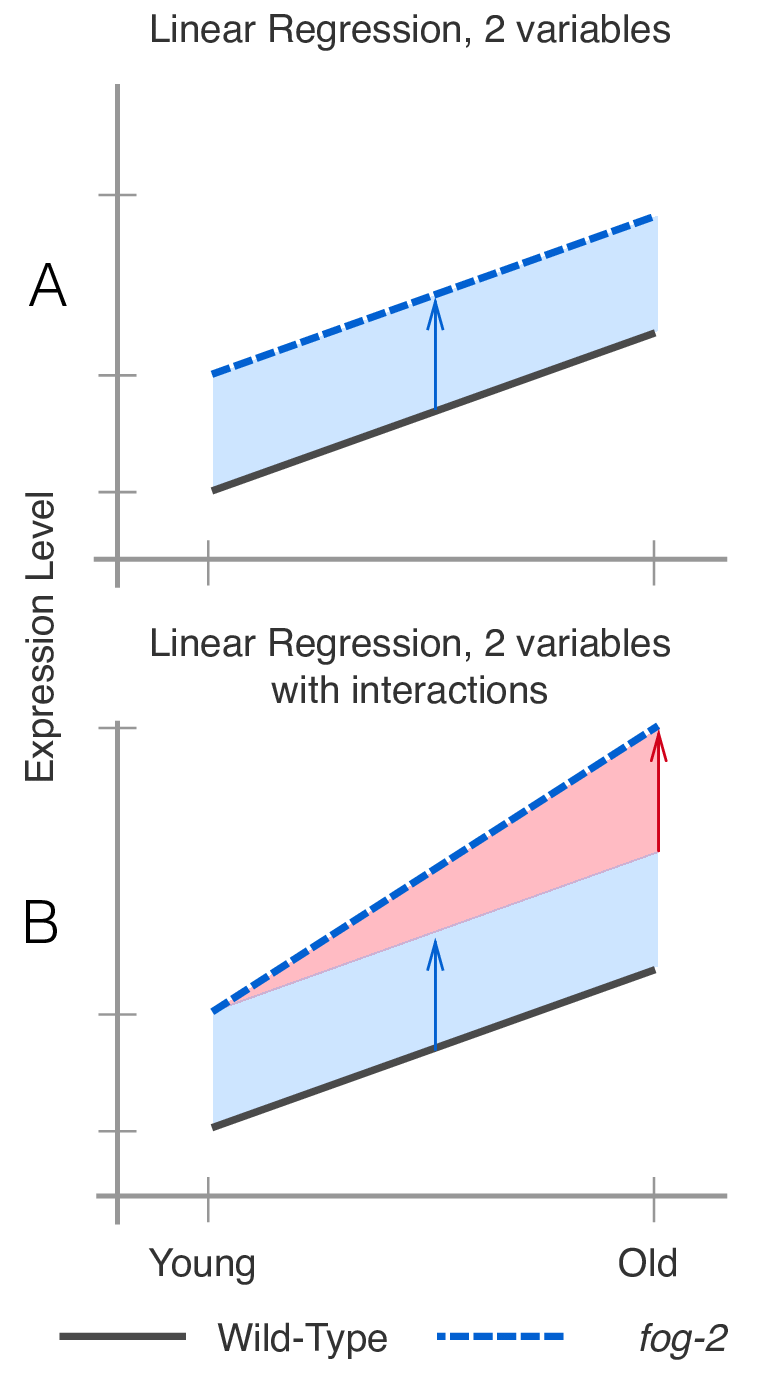
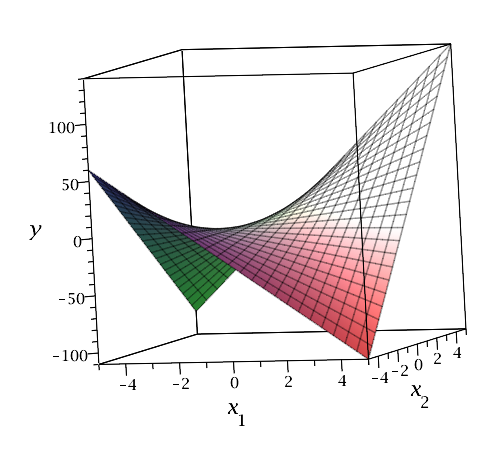
Multicolinealidad

---

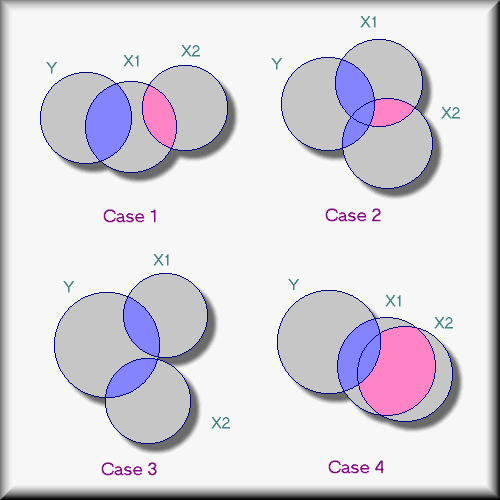
Detección de multicolinealidad

---

• ¿Cómo detectarla o inferirla?
  • Matriz de correlación
  • Pruebas estadísticas (Factor Inflacionario de Varianza - VIF)
  • Valores de VIF mayores a 5 o 10 son indicios de sesgo en la estimación de los coeficientes.

\[VIF = \frac{1}{1-R^2_p}\]

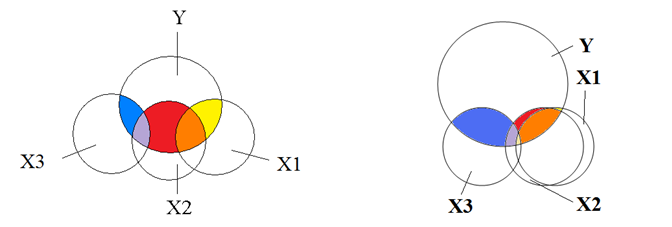
Selección de variables

---

Métodos de selección

---

• ¿Cómo comparar modelos?
  • RMSE
  • Criterios de información estadística:
    • \(LogLik\): logaritmo de la verosimilitud
    • \(AIC = -2 \times logLik + k + n\)
    • \(BIC = AIC,\ con\ k = log(n)\)

🤝🙂🤝