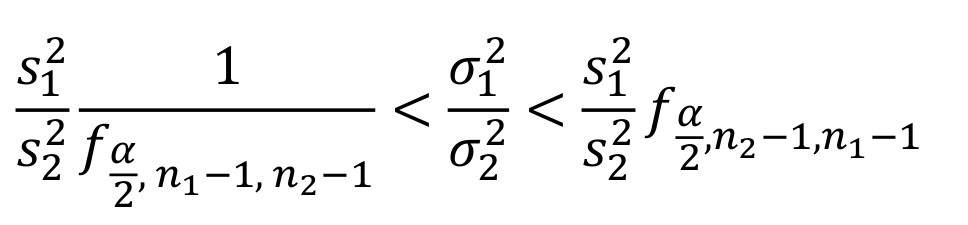
Inferencia Estadística
Diseño Experimental
2024-10-17
Inferencia
Inferencia
- Métodos de inferencia estadística:
- Clásico
- Bayesiano
- Inferencia:
- Estimación
- Puntual
- Intervalos
- Pruebas de hipótesis
- Estimación
- Parámetro: medida numérica que se obtiene con todos los datos de la población. Los parámetros generalmente son desconocidos.
- Estadístico: medida numérica que se obtiene de las muestras con determinado nivel de variación entre muestras.
- Inferencia estadística: proceso mediante el cual se generalizan conclusiones a la población, cuyo punto de partida son las muestras. Objetivos de la inferencia estadística:
- Estimación de parámetros
- Estimación puntual
- Intervalos de confianza
- Pruebas de hipótesis o test de significancia estadística
- Estimación de parámetros
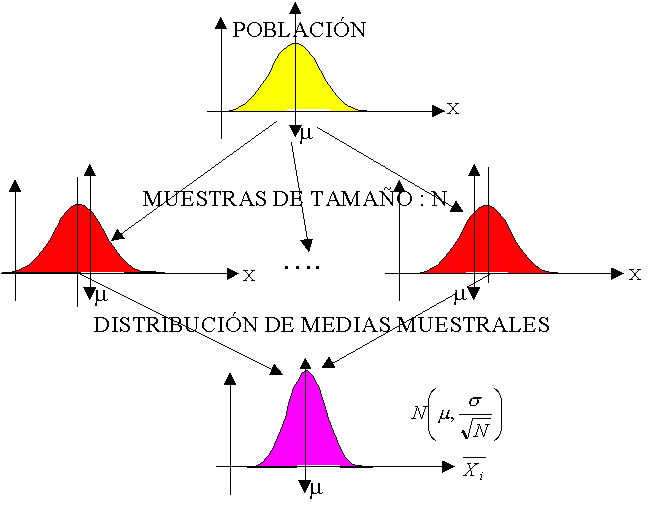
- Un estadístico muestral, proveniente de una muestra aleatoria, tiene un patrón de comportamiento (predecible) en repetidas muestras, dicho patrón se conoce como la distribución muestral del estadístico.
- Si se conoce la distribución muestral, es posible hacer inferencia estadística.
Estimación de parámetros
Tipos de estimación
- Nivel \(\alpha\) de uso frecuente:
- 0.10
- 0.05
- 0.01
- Nivel de confianza de uso frecuente:
- 0.90
- 0.95
- 0.99
- \(NC + \alpha = 1\)
Intervalos de confianza
Ejemplo con un \(NC = 97\%(0.97)\) y \(\alpha = 3\%(0.03)\)
- Para una muestra:
- \(\mu\)
- \(p\)
- \(\sigma^2\)
- Asociación de variables:
- \(\rho\)
- \(\beta\)
- Para dos muestras:
- \(\mu_1 - \mu_2\)
- \(\mu_1 - \mu_2\ (pareadas)\)
- \(p_1-p_2\)
- \(\sigma^2_1/\sigma^2_2\)
Pruebas de Hipótesis
Pruebas de hipótesis
- Para una muestra:
- \(\mu\)
- \(p\)
- \(\sigma^2\)
- Asociación de variables:
- \(\rho\)
- \(\beta\)
- Para dos muestras:
- \(\mu_1 - \mu_2\)
- \(\mu_1 - \mu_2\ (pareadas)\)
- \(p_1-p_2\)
- \(\sigma^2_1/\sigma^2_2\)
- Definir la hipótesis nula y la alternativa
- Tomar la muestra (muestreo)
- Calcular el estadístico (evidencias)
- Determinar el nivel \(\alpha\)
- Calcular el valor P
- Concluir (toma de decisiones)
Tipos de errores
- \(\alpha\): máxima probabilidad de cometer el error tipo I
- Potencia de la prueba \((1- \beta)\): probabilidad de rechazar una hipótesis nula que es falsa.
Valor p
- Se puede definir como la probabilidad exacta de cometer el error tipo I.
- Probabilidad de obtener un estadístico de prueba (evidencias) igual al que se obtuvo o más extremo.
- Es la probabilidad calculada, suponiendo que la hipótesis nula es verdadera, de obtener un estadístico de prueba tan discrepante a \(H_0\) como el valor que en realidad se obtuvo.
- En la medida que el valor P se hace más pequeño, más contradictorios son los datos con \(H_0\)
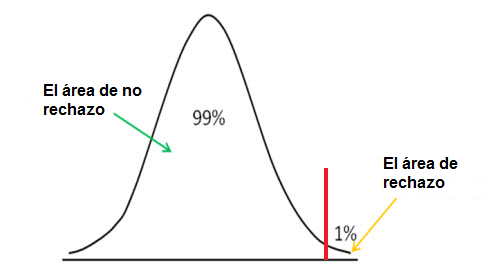
Conclusión en pruebas de hipótesis
- Contraste de hipótesis:
- Intervalos de confianza
- Región de rechazo
- Valor P
Métodos estadísticos

| Tipo de análisis | Método Paramétrico | Método no Paramétrico |
|---|---|---|
| Correlación | Pearson | Spearman o Kendall |
| Comparar medias (2 grupos) | t-Student | Wilcoxon |
Normalidad
Variación del muestreo: Bootstrapping

Inferencia sobre una población
Prueba de hipótesis para \(\mu\)
- Comprobar que la variable aleatoria se distribuye de forma normal.
- Definir la hipóteis nula y alternativa: \[H_0: nula\] \[H_1: alternativa\]
- Calcular el estadístico \[t = \frac{\bar{X}- \mu_0}{s/\sqrt{n}}\]
- Definir el error tipo I \(\alpha\)
- Calcular el valor P en una distribución \(t-student\) con \(n-1\) grados de libertad
- Comparar el valor P con \(\alpha\) y concluir.
Intervalos de confianza para \(\mu\)
Si \(\bar{x}\) es la media de una muestra aleatoria de tamaño \(n\) de una población normal con varianza \(\sigma^2\) conocida, un intervalo de confianza del \((1-\alpha)100\%\) para \(\mu\) está dado por la siguiente expresión:
.png)
.png)
- Nivel de confianza (NC) y \(\alpha\): \(Z_{\alpha/2}\):
- \(NC = 90\%,\ y\ \alpha = 0.10: Z_{\alpha/2} = 1.645\)
- \(NC = 95\%,\ y\ \alpha = 0.05: Z_{\alpha/2} = 1.960\)
- \(NC = 99\%,\ y\ \alpha = 0.01: Z_{\alpha/2} = 2.576\)
Si \(\bar{x}\) es la media de una muestra aleatoria de tamaño \(n\) de una población normal con varianza \(\sigma^2\) desconocida, un intervalo de confianza del \((1-\alpha)100\%\) para \(\mu\) está dado por la siguiente expresión:
.png)
Inferencia sobre \(p\)
Prueba de hipótesis para \(p\)
- Definir la hipótesis nula y alternativa \[H_0: nula\] \[H_1: alternativa\]
- Calcular el estadístico \[Z_0 = \frac{\hat{p}-p_0}{\sqrt{\frac{p_0(1-p_0)}{n}}}\]
- Definir el error tipo I \(\alpha\)
- Calcular el valor P en una distribución normal estándar
- Comparar el valor P con \(\alpha\) y concluir.
Intervalo de confianza para \(p\)
Si \(\hat{p}\) es la proporción de éxitos en una muestra aleatoria de tamaño \(n\), un intervalo de confianza del \((1-\alpha)100\%\) para \(p\) está dado por la siguiente expresión:
\[\hat{p}-Z_{\alpha/2}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}} < p < \hat{p}+Z_{\alpha/2}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}\]
Inferencia sobre \(\sigma_1^2/\sigma_2^2\)
Prueba de hipótesis para \(\sigma_1^2/\sigma_2^2\)
Previamente:
- Comprobar normalidad
Luego:
- Definir la hipótesis nula y alternativa
- Calcular el estadístico
\[F = \frac{S_1^2}{S_2^2}\]
- Definir el error tipo I \(\alpha\)
- Calcular el valor P
- Comparar el valor P con \(\alpha\) y concluir
Intervalo de confianza para \(\sigma^2_1/\sigma^2_2\)
Si \(S^2_1\) y \(S^2_2\) son las varianzas muestrales de muestras aleatorias independientes de tamaño \(n_1\) y \(n_2\) de poblaciones normales, un intervalo de confianza del \((1-\alpha)100\%\) para \(\sigma^2_1/\sigma^2_2\) está dado por la siguiente expresión:
Inferencia sobre \(\mu_1 - \mu_2\)
\(\mu_1 - \mu_2\), \(\sigma\) desconocidas e iguales
- Comprobar la normalidad.
- Definir la hipótesis nula y alternativa.
- Calcular el estadístico \[t = \frac{\bar{x_1}-\bar{x_2}-\delta_0}{S_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}\]
Donde: \[S_p = \frac{(n_1-1)S_1^2+(n_2-1)S_2^2}{n_1+n_2-2}\]
- Definir el error tipo I \(\alpha\)
- Calcular el valor P en una distribución \(t-student\) con \(n_1+n_2-2\) grados de libertad
- Comparar el valor P con \(\alpha\) y concluir.
\(\mu_1 - \mu_2\), \(\sigma\) desconocidas y diferentes
- Comprobar la normalidad y la homocedasticidad (igualdad de varianzas)s.
- Definir la hipótesis nula y alternativa.
- Calcular el estadístico \[t = \frac{\bar{x_1}-\bar{x_2}-\delta_0}{\sqrt{\frac{S_1^2}{n_1}+\frac{S_2^2}{n_2}}}\]
Donde \(t \sim t_v\), con grados de libertad \(v\):
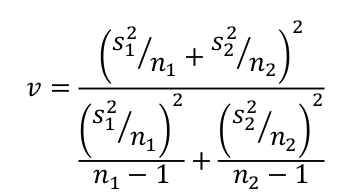
- Definir el error tipo I \(\alpha\)
- Calcular el valor P y concluir
Intervalos de confianza para \(\mu_1 - \mu_2\)
Varianzas conocidas
Si \(\bar{X_1}\) y \(\bar{X_2}\) son las medias muestrales de dos muestras aleatorias independientes de tamaño \(n_1\) y \(n_2\) de poblaciones normales con varianzas conocidas \(\sigma^2_1\) y \(\sigma^2_2\), respectivamente, un intervalo de confianza del \((1-\alpha)100\%\) para \(\mu_1-\mu_2\) está dado por la siguiente expresión:
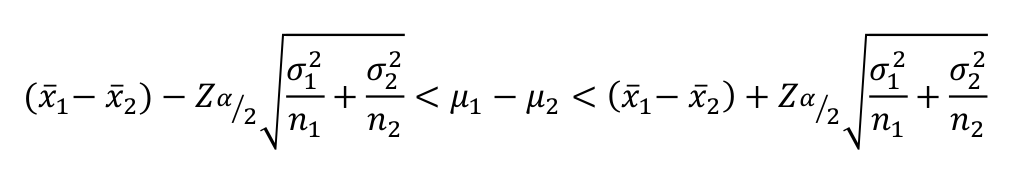
V. Desconocidas e iguales
Si \(\bar{X_1}\) y \(\bar{X_2}\) son las medias muestrales de dos muestras aleatorias independientes de tamaño \(n_1\) y \(n_2\) de poblaciones normales con varianzas desconocidas e iguales, un intervalo de confianza del \((1-\alpha)100\%\) para \(\mu_1-\mu_2\) está dado por la siguiente expresión:
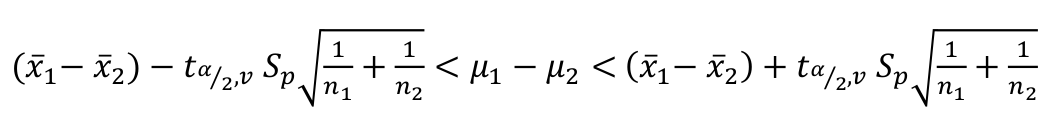
Donde \(v = n_1 + n_2 - 2\) y \(S_p\):
\[S_p = \frac{(n_1-1)S_1^2+(n_2-1)S_2^2}{n_1+n_2-2}\]
. Desconocidas y diferentes
Si \(\bar{X_1}\) y \(\bar{X_2}\) son las medias muestrales de dos muestras aleatorias independientes de tamaño \(n_1\) y \(n_2\) de poblaciones normales con varianzas diferentes y desconocidas, un intervalo de confianza del \((1-\alpha)100\%\) para \(\mu_1-\mu_2\) está dado por la siguiente expresión:
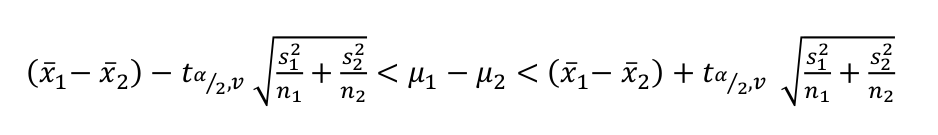
Donde \(v\):
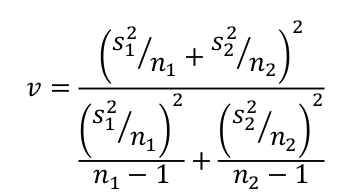
Inferencia sobre \(\hat{p_1}-\hat{p_2}\)
Prueba de hipótesis para \(\hat{p_1}-\hat{p_2}\)
- Definir la hipóteis nula y alternativa
- Calcular el estadístico \[z = \frac{\hat{p_1}-\hat{p_2}}{\sqrt{\frac{p_1(1-p_1)}{n_1}+\frac{p_2(1-p_2)}{n_2}}}\]
- Definir el error tipo I \(\alpha\)
- Calcular el valor P en una distribución normal estándar (\(z\))
- Comparar el valor P con \(\alpha\) y concluir.
Intervalo de confianza para \(\hat{p_1}-\hat{p_2}\)
Si \(\hat{p_1}\) y \(\hat{p_2}\) son las proporciones de éxito de dos muestras aleatorias independientes de tamaño \(n_1\) y \(n_2\), entonces un intervalo del \((1-\alpha)100\%\) para \(\hat{p_1}-\hat{p_2}\) está dado por la siguiente expresión:
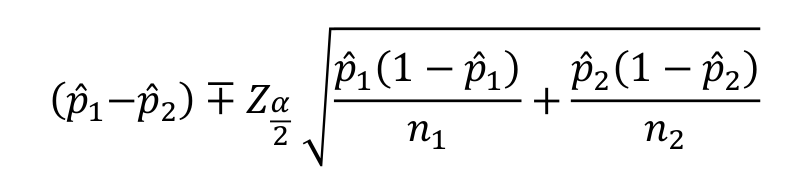
¡Gracias!

