Análisis de Experimentos
Diseño Experimental
Edimer David Jaramillo
2024-11-22
Inferencia Estadística
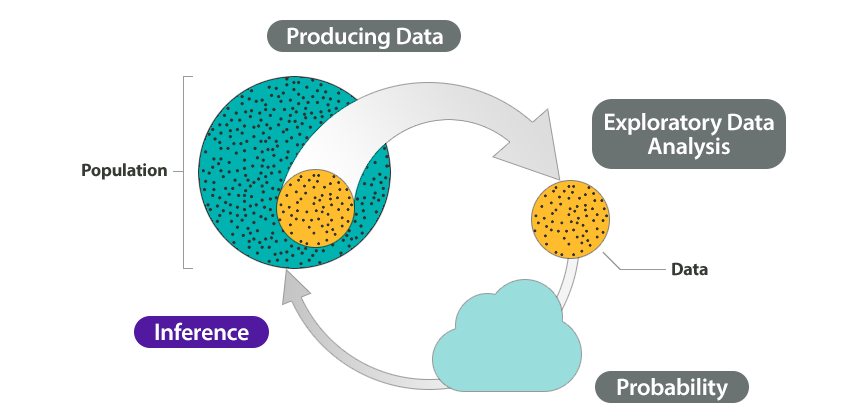
¿Cómo comparar más de 2 grupos?
\[y_{ij} = \mu + \tau_j + \epsilon_{ij}\]
Donde:
- \(y_{ij}\): variable respuesta o dependiente
- \(\mu\): media general
- \(\tau_{J}\): efecto del \(j-ésimo\) tratamiento
- \(\epsilon_{ij}\): error aleatorio experimental, se debe garantizar que \(\epsilon_{ij} \sim N(\mu=0,\sigma^2)\)

Tipos de diseños
Diseño Completamente al Azar (DCA)
\[y_{ij} = \mu + \tau_j + \epsilon_{ij}\]
Donde:
- \(y_{ij}\): variable respuesta o dependiente
- \(\mu\): media general
- \(\tau_{j}\): efecto del \(j-ésimo\) tratamiento
- \(\epsilon_{ij}\): error aleatorio experimental, se debe garantizar que \(\epsilon_{ij} \sim N(\mu=0,\sigma^2)\)
Diseño en Bloques al Azar (DBA)
\[y_{ijk} = \mu + \tau_j + \beta_k + \epsilon_{ijk}\]
Donde:
- \(y_{ijk}\): variable respuesta o dependiente
- \(\mu\): media general
- \(\tau_{j}\): efecto del \(j-ésimo\) tratamiento
- \(\beta_k\): efecto del \(k-ésimo\) tratamiento
- \(\epsilon_{ijk}\): error aleatorio experimental, se debe garantizar que \(\epsilon_{ijk} \sim N(\mu=0,\sigma^2)\)
Diseños factoriales

- Modelo aditivo:
\[y_{ij...} = \mu + \tau_j + \tau_j + ... + \tau_j + \epsilon_{ij...}\]
- Modelo multiplicativo:
\[y_{ij...} = \mu + (\tau \tau)_{jk} + ... + \epsilon_{ij...}\]
Representación Diseños Factoriales

¡Gracias!

